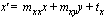
The following functions create transformation objects that can be used, for instance, in a call to compose-transformations . The transformation constructors do not capture any of their inputs. The constructors all create objects that are subclasses of transformation .
make-translation-transformation [Function]
Arguments: translation-x translation-y
Summary: A translation is a transformation that preserves the length, angle, and orientation of all geometric entities.
make-translation-transformation returns a transformation that translates all points by translation-x in the x direction and translation-y in the y direction. translation-x and translation-y must be real numbers.
make-rotation-transformation [Function]
Arguments: angle
&optional
origin
make-rotation-transformation* [Function]
Arguments: angle
&optional
origin-x origin-y
Summary: A rotation is a transformation that preserves the length and angles of all geometric entities. Rotations also preserve one point (the origin) and the distance of all entities from that point.
make-rotation-transformation returns a transformation that rotates all points by angle (which is a real number indicating an angle in radians) around the point origin . If origin is supplied it must be a point; if not supplied, it defaults to (0, 0). origin-x and origin-y must be real numbers.
make-scaling-transformation [Function]
Arguments: scale-x scale-y
&optional
origin
make-scaling-transformation* [Function]
Arguments: scale-x scale-y
&optional
origin-x origin-y
Summary: As discussed previously, there is no single definition of a scaling transformation. make-scaling-transformation returns a transformation that multiplies the x -coordinate distance of every point from origin by scale-x and the y -coordinate distance of every point from origin by scale-y . scale-x and scale-y must be real numbers. If origin is supplied it must be a point; if not supplied, it defaults to (0, 0). origin-x and origin-y must be real numbers.
make-reflection-transformation [Function]
make-reflection-transformation* [Function]
Summary: A reflection is a transformation that preserves lengths and magnitudes of angles, but changes the sign (or "handedness") of angles. If you think of the drawing plane on a transparent sheet of paper, a reflection is a transformation that "turns the paper over."
make-reflection-transformation returns a transformation that reflects every point through the line passing through the points point1 and point2 (or through the positions (x1, y1) and (x2, y2) in the case of the spread version).
make-transformation [Function]
Arguments: m xx m xy m yx m yy t x t y
Summary: Returns a general transformation whose effect is:
where
x
and
y
are the coordinates of a point before the transformation 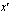and 
and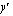 
are the coordinates of the corresponding point after.
All of the arguments to make-transformation must be real numbers.
make-3-point-transformation [Function]
Arguments: point-1 point-2 point-3 point-1-image point-2-image point-3-image
Summary: Returns a transformation that takes points point-1 into point-1-image , point-2 into point-2-image , and point-3 into point-3-image . Three non-collinear points and their images under the transformation are enough to specify any affine transformation.
If point-1 , point-2 , and point-3 are collinear, the transformation-underspecified error will be signaled. If point-1-image , point-2-image , and point-3-image are collinear, the resulting transformation will be singular (that is, will have no inverse), but this is not an error.
make-3-point-transformation* [Function]
Arguments: x1 y1 x2 y2 x3 y3 x1-image y1-image x2-image y2-image x3-image y3-image
Summary: Returns a transformation that takes the points at the positions ( x1 , y1 ) into ( x1-image , y1-image ), ( x2 , y2 ) into ( x2-image , y2-image ) and ( x3 , y3 ) into ( x3-image , y3-image ). Three non-collinear points and their images under the transformation are enough to specify any affine transformation.
If the positions (x1, y1) , (x2, y2) , and (x3, y3) are collinear, the transformation-underspecified error will be signaled. If ( x1-image , y1-image ), ( x2-image , y2-image ), and ( x3-image , y3-image ) are collinear, the resulting transformation will be singular, but this is not an error.
This is the spread version of make-3-point-transformation .
